Volume

This module contains layers working with volumetric representation of proteins.

Computes the 3D atomic densities of each atom type. Let's denote the position of the $j$-th atom of type $i$ as $\mathbf{x}_{ij}$. The volumetric density for atom type $i$ reads: $$ V_i(\mathbf{r}) = \sum_j \exp\left( -\frac{|\mathbf{r} - \mathbf{x}_{ij}|^2}{2\sigma^2} \right) $$ The value of $\sigma$ is set to 1 grid unit. To reduce the amount of computation, the contribution of each atom is considered only up to 2 grid cells away from its position.

Input/Output

Example


import torch
from TorchProteinLibrary import Volume, FullAtomModel
import _Volume
import numpy as np
import matplotlib.pylab as plt
import mpl_toolkits.mplot3d.axes3d as p3

if __name__=='__main__':
		a2c = FullAtomModel.Angles2Coords()
		translate = FullAtomModel.CoordsTranslate()
		sequences = ['GGMLGWAHFGY']
		
		#Setting conformation to alpha-helix
		angles = torch.zeros(len(sequences), 7, len(sequences[-1]), dtype=torch.double, device='cpu')
		angles.data[:,0,:] = -1.047 # phi = -60 degrees
		angles.data[:,1,:] = -0.698 # psi = -40 degrees
		angles.data[:,2:,:] = 110.4*np.pi/180.0
		
		#Converting angles to coordinates
		coords, res_names, atom_names, num_atoms = a2c(angles, sequences)
		
		#Translating the structure to fit inside the volume
		translation = torch.tensor([[60, 60, 60]], dtype=torch.double, device='cpu')
		coords = translate(coords, translation, num_atoms)
		
		#Converting to typed coords manually
		#We need dimension 1 equal to 11, because right now 11 atom types are implemented and
		#this layer expects 11 offsets and 11 num atoms of type per each structure
		coords = coords.to(dtype=torch.double, device='cuda')
		num_atoms_of_type = torch.zeros(1, 11, dtype=torch.int, device='cuda')
		num_atoms_of_type.data[0,0] = num_atoms.data[0]
		offsets = torch.zeros(1, 11, dtype=torch.int, device='cuda')
		offsets.data[:,1:] = num_atoms.data[0]
		
		#Projecting to volume
		tc2v = Volume.TypedCoords2Volume(box_size=120)
		volume = tc2v(coords, num_atoms_of_type, offsets)
		
		#Saving the volume to a file, we need to sum all the atom types, because
		#Volume2Xplor currently accepts only 3d volumes
		volume = volume.sum(dim=1).to(device='cpu').squeeze()
		_Volume.Volume2Xplor(volume, "volume.xplor")
...
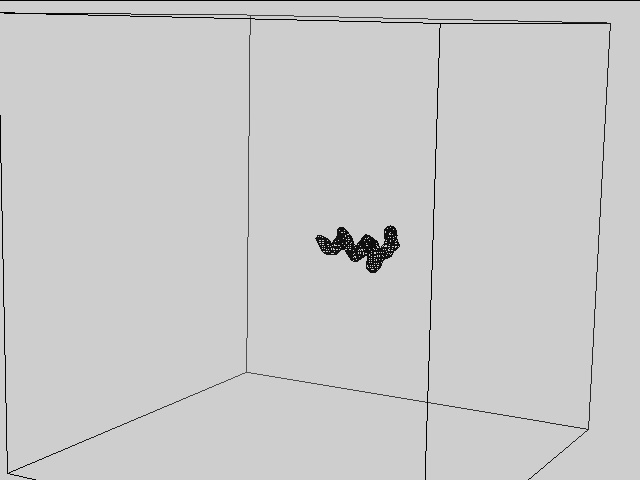
Extracts local features from a set of volumes based on the atomic coordinates, scaled according to proportion of initial volume size (box_size_bins) and current volume size (box_size_ang). This process is illustrated on the image below:

...

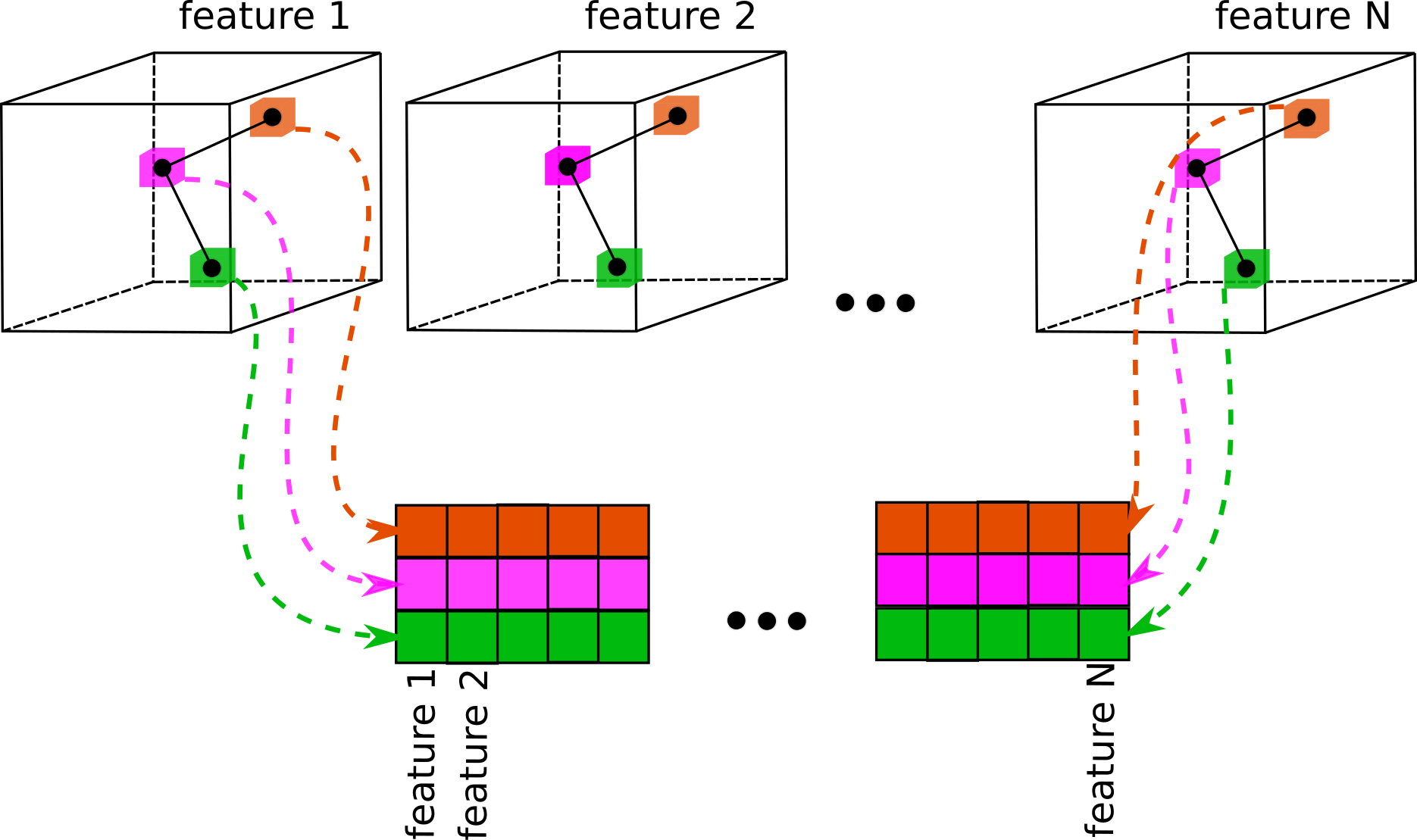
In version 0.1 of the library, this layer is not differentiable.

Input/Output

Computes the correlation between two sets of volumes of the same size. Let's denote feature $i$ volume as $V_i$. The correlation between two sets of volumes is: $$ Corr_i = (V^{(1)}_i * V^{(2)}_i) $$ where $$ (V^{(1)}_i * V^{(2)}_i) (x,y,z) = \sum_{klm} V^{(1)}_i (k,l,m) V^{(1)}_i (k+x,l+y,m+z) $$ We will denote the translation of the second volume wrt the first as $\vec{\tau} = (x, y, z)$

Implementation

First we pad volumes to twice their sizes to avoid circular terms. Then we compute the correlation using FFT: $$ (V^{(1)}_i * V^{(2)}_i) (\vec{\tau}) = IFFT \left[ FFT(V^{(1)}_i) \cdot conj(FFT(V^{(2)}_i)) \right] $$ The derivative of a function $L$, that depends on the correlation is: $$\begin{eqnarray} \frac{\partial L }{\partial V^{(1)}_i } &=& \frac{\partial L}{\partial (V^{(1)}_i * V^{(2)}_i)} * conj(V^{(2)}_i) \\ \frac{\partial L }{\partial V^{(2)}_i } &=& V^{(1)}_i * \frac{\partial L}{\partial (V^{(1)}_i * V^{(2)}_i)} \end{eqnarray} $$ This layer is implemented using cuFFT. It should be taken into account that the correlation is circular, therefore the output has circular structure. Let's denote $r_i$ to be the coordinates of a cell in the output volume, then the translation of the second volume wrt the first ($\vec{\tau}$) will have coordinates: $$ \tau_i = \begin{cases} r_i & r_i < \mbox{box_size}, \\ r_i - 2\cdot\mbox{box_size} & r_i \ge \mbox{box_size} \end{cases} $$

Input/Output